

Blowup and Non-Lipschitz singularities in ODEs and PDEs, post-blowup dynamics, spontaneously stochastic solutions
We consider a class of ordinary differential equations featuring a non-Lipschitz singularity at the origin. Solutions of such systems are unique up until they hit the origin, which we term 'blowup'. However, infinitely many solutions may exist for longer times. We introduce physically motivated regularizations by smoothing the vector field in a ν-ball around the origin and then taking the limit ν→0. We show that this limit can be understood using a solution-dependent renormalization procedure, which maps the pre-blowup dynamics to the solution ending at infinitely large renormalized time and the post-blowup dynamics to a different renormalized solution starting infinitely far in the past. The ν-regularization establishes a relation between these two different "lives" of the renormalized system. We prove that, in some generic situations, this procedure selects a unique global solution (or a family of solutions), which does not depend on the details of the regularization.
T.D. Drivas and A.A. Mailybaev, "Life after death" in ordinary differential equations with a non-Lipschitz singularity, (2018). ArXiv: 1806.09001. [PDF] [Link]


We study the inviscid limit of the Rayleigh-Taylor turbulence in 2D and 3D using direct numerical simulations and with specially designed shell models. We show that the dynamics can be represented as a stochastic traveling wave in logarithmic space-time variables. The results are extended to the case of non-uniform initial conditions.
L. Biferale, G. Boffetta, A.A. Mailybaev and A. Scagliarini, Rayleigh-Taylor turbulence with singular non-uniform initial conditions, Physical Review Fluids 3 (2018), 092601(R). [PDF] [Link]
A.A. Mailybaev, Toward analytic theory of the Rayleigh-Taylor instability: lessons from a toy model, Nonlinearity 30 (2017), 2466-2484. [Link] [PDF]
We study the inviscid limit of the Sabra shell model of turbulence, which is considered as a particular case of a viscous conservation law in one space dimension with a nonlocal quadratic flux function. This model has a self-similar finite time blowup. It is shown that the post-blowup dynamics can associated with an attractor of the renormalized system. This attractor is periodic for the real Sabra model (providing a one-parameter family of the inviscid solutions) and it is chaotic for the complex model (providing a unique spontaneously stochastic inviscid solution)
A.A. Mailybaev, Spontaneous stochasticity of velocity in turbulence models, Multiscale Modeling and Simulation (SIAM) 14 (2016), 96-112. [Link] [PDF]
A.A. Mailybaev, Spontaneously stochastic solutions in one-dimensional inviscid systems, Nonlinearity 29 (2016), 2238-2252. [Link] [PDF]

Exceptional points in non-Hermitian systems, applications in optics and quantum physics
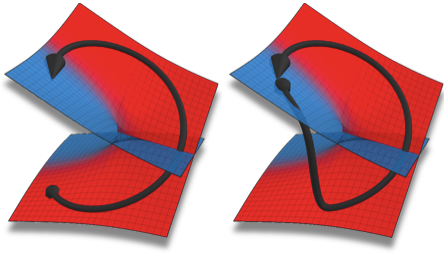
Systems with loss or gain have resonant modes that decay or grow with time. Whenever two such modes coalesce both in their resonant frequency and their rate of decay or growth, an ‘exceptional point’ occurs. We present an experiment with a waveguide that steers incoming waves around an exceptional point during the transmission. The induced transitions transform this device into an asymmetric switch between different waveguide modes.
J. Doppler, A.A. Mailybaev, J. Böhm, U. Kuhl, A. Girschik, F. Libisch, T.J. Milburn, P. Rabl, N. Moiseyev, S. Rotter, Dynamically encircling an exceptional point for asymmetric mode switching, Nature (2016) 537:7618, 76-79.
[Link] [Online version] Supplementary material [PDF]
Selected for: Nature Physics News & Views.
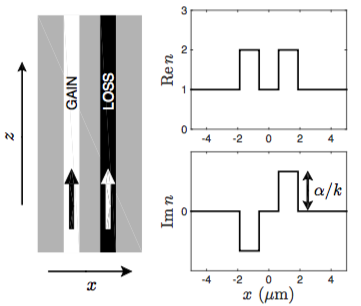
Almost twenty years ago the light was slowed down to less than 10−7 of its vacuum speed in a cloud of ultracold atoms. Here we extend the phenomenon of stopped light to the new field of parity-time (PT) symmetric systems. We show that zero group speed in PT symmetric optical waveguides can be achieved if the system is prepared at an exceptional point, where two optical modes coalesce.
T. Goldzak, A.A. Mailybaev and N. Moiseyev, Light stops at exceptional points, Physical Review Letters 120 (2018), 013901. [Link] [PDF]
Described in Newsweek, The Independent, Daily Mail, Phys.org, Science Alert, Europa press, International Business Times, Live Science.
In Portuguese: IMPA's press release, Destaque em SBF, Revista Pesquisa Fapesp
Blowup phenomena in hydrodynamics, mechanism of developed turbulence, shell and other simplified models
Here we propose a new model formally identical to incompressible Euler equations, by imitating the calculus on a 3D logarithmic lattice. Blowup in this model is explained as a chaotic attractor in renormalized variables. This attractor spans the anomalously large interval of over six-decades of spatial scales. For the original Euler system, our results suggest that the existing DNS strategies at the resolution accessible now (and presumably in a rather long future) are unsuitable, by far, for the blowup analysis.
C.S. Campolina and A.A. Mailybaev, Chaotic blowup in the 3D incompressible Euler equations on a logarithmic lattice, Physical Review Letters 121 (2018), 064501. [PDF] [Link] [Supplementary video]
We discuss a theoretical framework to define an optimal sub-grid closure for shell models of turbulence. The closure is based on the ansatz that consecutive shell multipliers are short-range correlated, following the third hypothesis of Kolmogorov formulated for similar quantities for the original three dimensional Navier-Stokes turbulence.
L. Biferale, A.A. Mailybaev and G. Parisi, An optimal subgrid scheme for shell models of turbulence, Phys. Rev. E 95 (2017), 043108. [Link] [PDF]

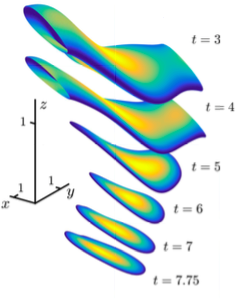
Incompressible 3D Euler equations develop high vorticity in very thin pancake-like regions from generic large-scale initial conditions. In this work we propose an exact solution of the Euler equations for the asymptotic pancake evolution.
D.S. Agafontsev, E.A. Kuznetsov and A.A. Mailybaev, Asymptotic solution for high vorticity regions in incompressible 3D Euler equations, Journal of Fluid Mechanics 813, R1 (2017). [Link] [PDF]
Singularities and instabilities
 Considering two-dimensional potential ideal flow with free surface and finite depth, we study the dynamics of small-amplitude and short-wavelength wavetrains propagating on the background of a steepening nonlinear wave. This can be seen as a model for small ripples developing on slopes of breaking waves in the surf zone. Using the concept of wave action as an adiabatic invariant, we derive an explicit asymptotic expression for the change of ripple steepness. We show that strong compression near the tip on the wave leads to an explosive (super-exponential) ripple instability. This instability may play important role for understanding fragmentation and whitecapping at the surface of breaking waves.
Considering two-dimensional potential ideal flow with free surface and finite depth, we study the dynamics of small-amplitude and short-wavelength wavetrains propagating on the background of a steepening nonlinear wave. This can be seen as a model for small ripples developing on slopes of breaking waves in the surf zone. Using the concept of wave action as an adiabatic invariant, we derive an explicit asymptotic expression for the change of ripple steepness. We show that strong compression near the tip on the wave leads to an explosive (super-exponential) ripple instability. This instability may play important role for understanding fragmentation and whitecapping at the surface of breaking waves.
A.A. Mailybaev and A. Nachbin, Explosive ripple instability due to incipient wave breaking, Journal of Fluid Mechanics 863, 876-892 (2019).
[Link] [PDF] Selected for the JFM cover
Photo courtesy of Keahi de Aboitiz. Click to see the YouTube video
Singular traveling waves in conservation laws, in-situ combustion, enhanced oil recovery (EOR)
This paper combines analytical and numerical studies of light oil recovery by air injection. Our solution shows that between regimes of total and partial oxygen consumption there is a change in the oxidation wave, which may have negative implications for oxygen breakthrough.
F.P. Santos, A.A. Mailybaev and D. Marchesin, Oxidation wave structure and oxygen breakthrough for air injection into light oil reservoirs, Computational Geosciences (2016) 20, 1095-1107. [Link] [PDF]
We study a nonlinear wave for a system of balance laws, which describes combustion for two-phase (gas and liquid) flow in a porous medium. The problem is formulated for a general N-component liquid for modeling multicomponent effects. Despite the immense complexity of the model, the problem allows an analytic solution. The clue to this solution is a special form of a folding singularity at an internal point of the wave profile.
M. A. Endo Kokubun and A.A. Mailybaev, Singularity of a combustion wave profile: a clue to the multicomponent theory for liquid-gas filtration, SIAM Journal on Applied Mathematics 77 (2017), 1375–1396. [Link] [PDF]
